小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分 ★こ円の面積の解説 円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr2 となります。 円の面積を求める公式 面積=半径×半径×円周率 半径3cmの円の面積は何cm 2 ? ※円周率を314とした場合 → 3cm×3cm× 円周の長さを出すために、まず円の直径を知る必要があります。 この円の面積が096㎠であることから 円の面積=半径×半径×314=096(㎠) 半径×半径=096÷314= 64 同じ数をかけて64になるのは8。 半径が8cmとわかったので、直径はその2倍の16cm
円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ
円の面積 円周 プリント
円の面積 円周 プリント- 円の面積πr^2を半径rで微分すると円周の長さ2πrとなる。 逆に 円周の長さ 2πr を 半径 r で積分すると 円の面積 πr^2 になる。 球の体積 4/3πr^3 を 半径 r で微分すると 球の表面積 4πr^2 、逆に 球の表面積 4πr^2 を 半径 r で積分すると球の体積** 4/3πr^3 となる。円の面積から半径を求める 円の面積から直径を求める 円の面積から円周 を求める 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。




円の面積の公式 算数の公式
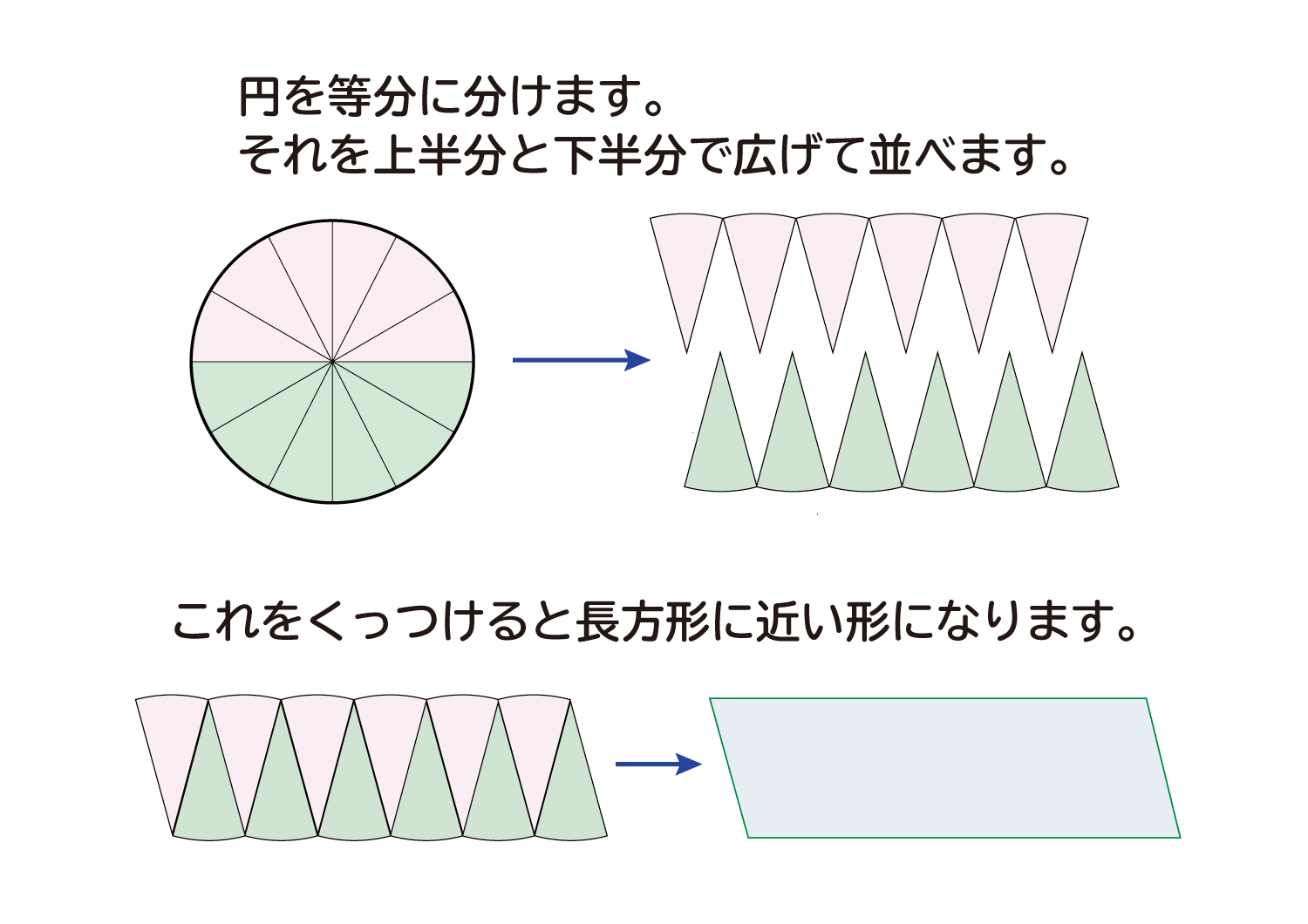
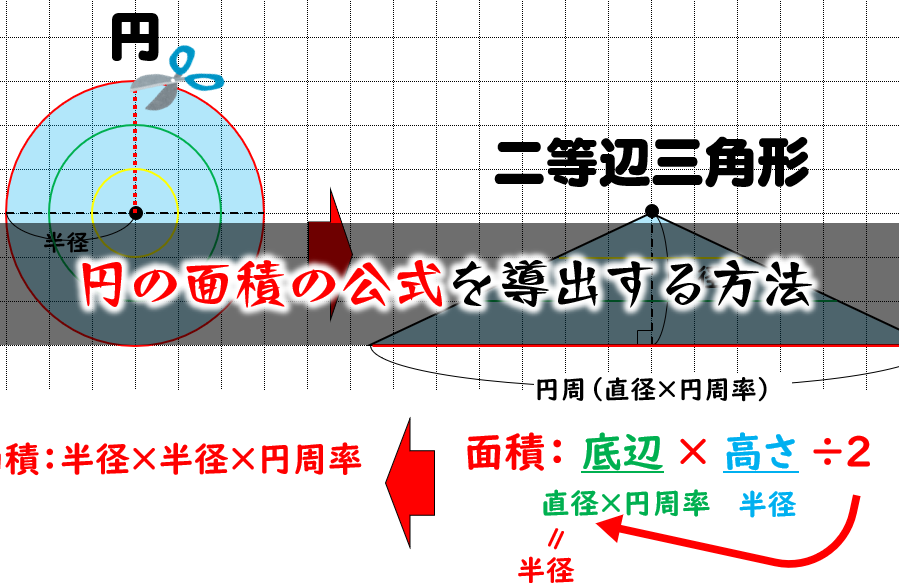
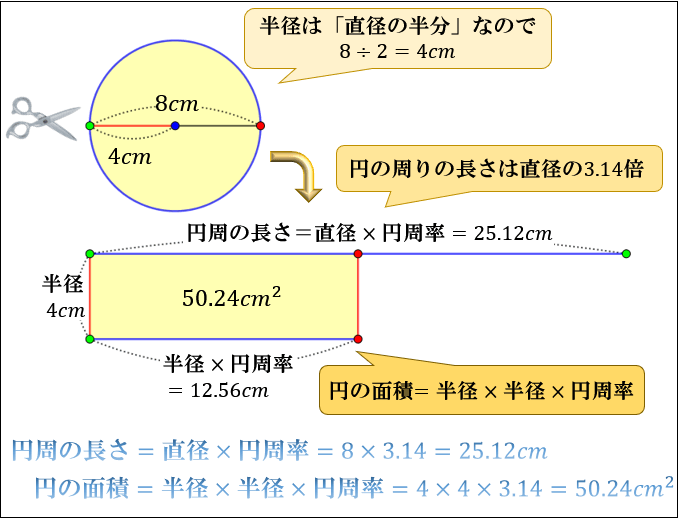
円の面積 複雑でよく間違える計算なので助かった。 食卓を買い替えるにあたり、丸ちゃぶ台サイズ90φか100φかかなり悩みました。 いっそ間をとって95φもありかなと思ったり。 ちなみに現テーブルは長方形90×60。 夫が現テーブルを手狭に感じている 円の面積の求め方公式 ~円の面積~ (半径)×(半径)×(円周率314) 円の面積公式を理解するためには、図形を見ながら考えていく必要があります。 円を分割して、並びかえると このように平行四辺形に近い形に変形することができるよね。 これ円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか
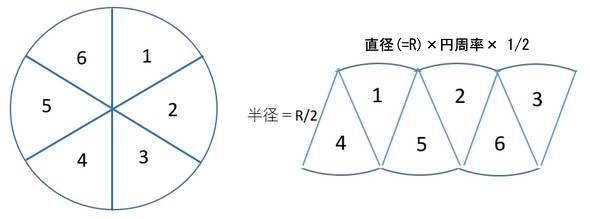
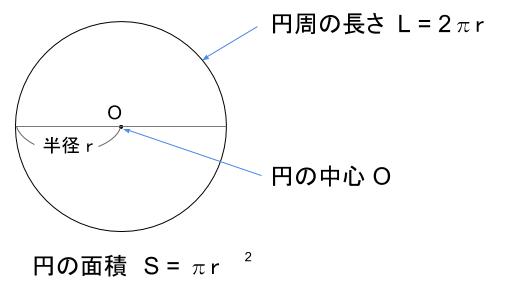
の面積は円周率 \(\pi\) に近づいてゆくはずです。 図1のように、赤い4角形各辺の垂直二等分線が円に交わる点を新たな頂点として追加すれば青い8角形が得られ, 同様に各辺の垂直二等分線によって緑の16角形が得られ、以下同様に 32角形, 64角形『よこ』は『円周の半分』 に置き換えられますよね? そして、円周は一番初めに説明したように で表せます。 なので、 円の面積=平行四辺形の面積 =たて×よこ =半径×円周の半分 と計算されて 円の面積=半径×半径×3.14 となるのです^^ 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積 A = πr2 A = π r 2 の式において、 r2 r 2 の 2 2 を
Java円周の長さと円の面積を求めるプログラム 8月 16, 21 / 最終更新日時 11月 1, 21 颯斗 Java このサンプルコードは、Javaの基礎をある程度勉強した人のためのサンプルコードで次に、上記の部分なのですが、ここでは、実際に入力された半径から円周と円の面積を計算するところになります。 実行結果 円の半径を入力してください。 23 円周はです。 円の面積はです。 円の半径を入力してください。 254 円周は15円の面積を求める公式は 円の面積 = 半径 × 半径 × 円周率 なので、半径を x とすると = x × x × 314 x × x = ÷ 314 x × x = 36 x = 6 ( c m) になります。



小学算数 円の半径と面積と円周の関係を理解しよう 偏差値40プログラマー




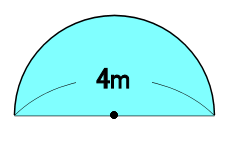
半円や4分の1の円 四分円 の面積を計算する方法 白丸くん
円の面積から半径を求める 円の面積から直径を求める 円の面積から円周 を求める 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。外周(円周)から直径の計算方法は?1分でわかる計算、直径5cm、6cmの円周 円の断面積から半径、直径を求める方法 円の断面積から半径、直径を求めましょう。円の断面積は100m㎡です。 円の断面積と直径の関係は下記でした。 A=(φ/2) 2 ×π よって、半径22cmの円の周の長さを求めよ。 半径12cmの円の面積を求めよ。 直径19cmの円の周の長さを求めよ。 直径15cmの円の面積を求めよ。 次の問いに答えよ。 円周の長さが14πcmの円の面積を求めよ。 円周の長さが8xπcmの円の面積を求めよ。 次の図の影をつけた



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




円の面積の公式 算数の公式
この問題のポイント ・ 円の面積は「半径×半径×円周率(314)」 という公式を使って求めます。 円の面積が、なぜ「半径×半径×円周率(314)」なのか、もし疑問に思ったときには、こちらに解説をしていますので、参考にしてみてください。 ここではImport numpy as np #numpyをインポート pi = nppi #変数piにnppiを代入 円周の長さから、直径・半径と円の面積を求める。 計算には、javascriptライブラリ BigNumberjs を使用しています。 円周率については、デフォルトでは314となっていますが、少数点14位まで自由に変更可能です。




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ
円周率が厳密に314であり、半径 \(r\) の円の面積が \(314r^2\) となる空間が構成できるかもしれないが、わからない。ちなみに、空間が曲がっている一般の曲面上では円周率は一定にはならない。全ての円が相似であるという条件が成立しないからだ。 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の円の半径を入力 r = 18 円の面積 S = 円周の長さ L = ここでは半径「10」、「18」の円の面積と円周の長さを計算してみました。 その他のサンプルプログラムも合わせてご覧ください。




インディアナ州円周率法案 Wikipedia




Circle1 小学校算数 円周と面積 Youtube
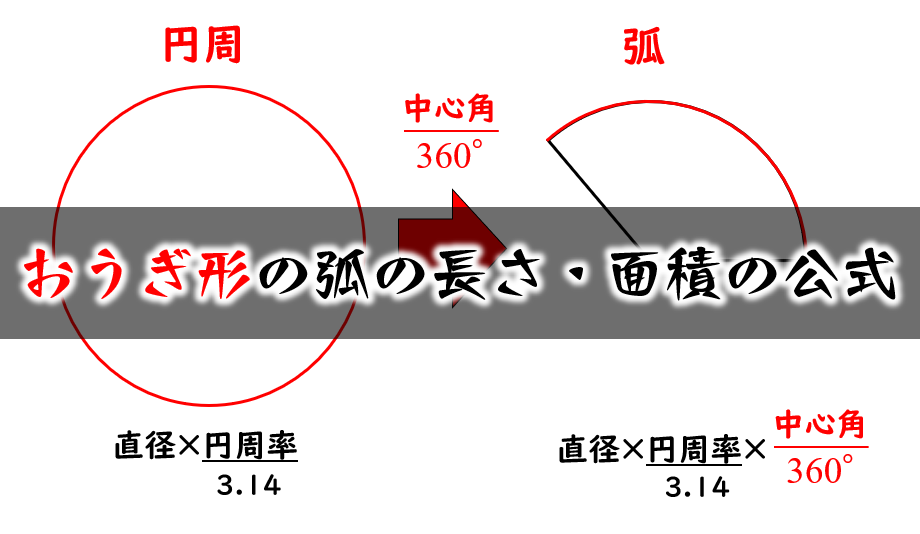
円の面積の公式 円の面積は 『半径×半径×円周率』 で計算できます。 たとえば以下のような問題の場合。 例題 半径 2cm 2 c m の円の面積を求めよ。 答えはこのように求めることができます。 2 ×2× 314=1256(cm2) 2 × 2 × 314 = 1256 ( c m 2) つづいて、なぜ 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さラジアンを使った円の面積と円周を求める 半径r、中心角θ (ラジアン)の扇型の孤の長さをl,扇型の面積をSとは、 中心角の角の大きさに比例する ので、 l= 2πr⋅ θ 2π l = 2 π r ⋅ θ 2 π 約分して l= rθ l = r θ 面積も同様にして S =πr2 ⋅ θ 2π S = π r 2 ⋅ θ 2



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ



P 3 05を証明せよ 東大の伝説の入試問題をプログラムで解く 組み込みエンジニアの現場力養成ドリル 27 3 5 ページ Techfactory
ここで、S は円の面積、π は円周率、r は円の半径を表します。 このページの続きでは、この公式の導き方のイメージと、円の面積を求める計算問題の解き方を説明しています。 小学生向けに文字を使わない説明もしているので、ぜひご覧ください。 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい円の面積は、半径×半径×円周率でで計算できます。円周率は「π(パイ)」と呼ばれ、その値は で、小数点以下は無限に続きます。 ここでは、キーボードから半径を入力して、円の面積を表示するプログラムを紹介します。
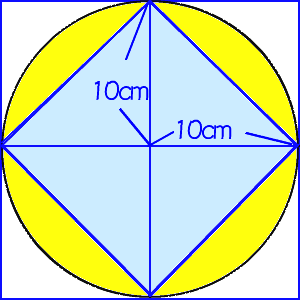



6年算数 円の面積 2 わかる教え方
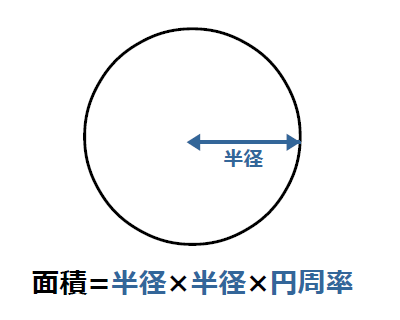



円の面積計算 ゆるゆるプログラミング
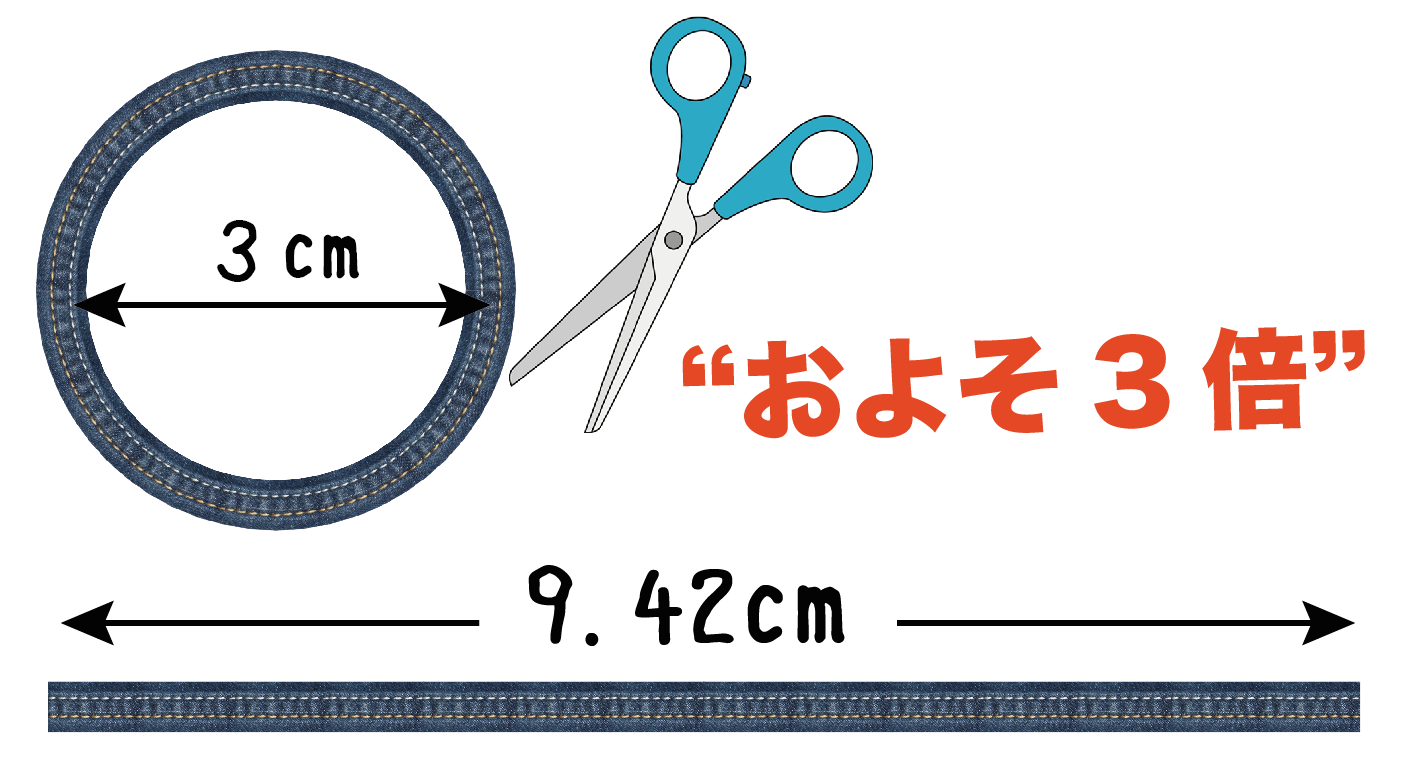
円周率 円周の長さが直径の何倍であるかを表す数 円の面積の公式の求め方 では、本題に入りましょう。なぜ円の面積は、 $$\text{円の面積} = \text{円周率}(314) \times \text{半径} \times \text{半径}$$ という公式で表せるのかを考えていきます。円周率の計算 おかけで短時間でできました。 ありがとうございます😭 大変に役に立ちました。 関孝和が、小数点以下11桁まで正確に計算して、円周率がより僅かに小さいことを突き止めた。 (今から300年ほど前) 3 円の面積の関数\( S(r) \)は微分すると円周になると言えるわけです(完璧さを求める方は\( h
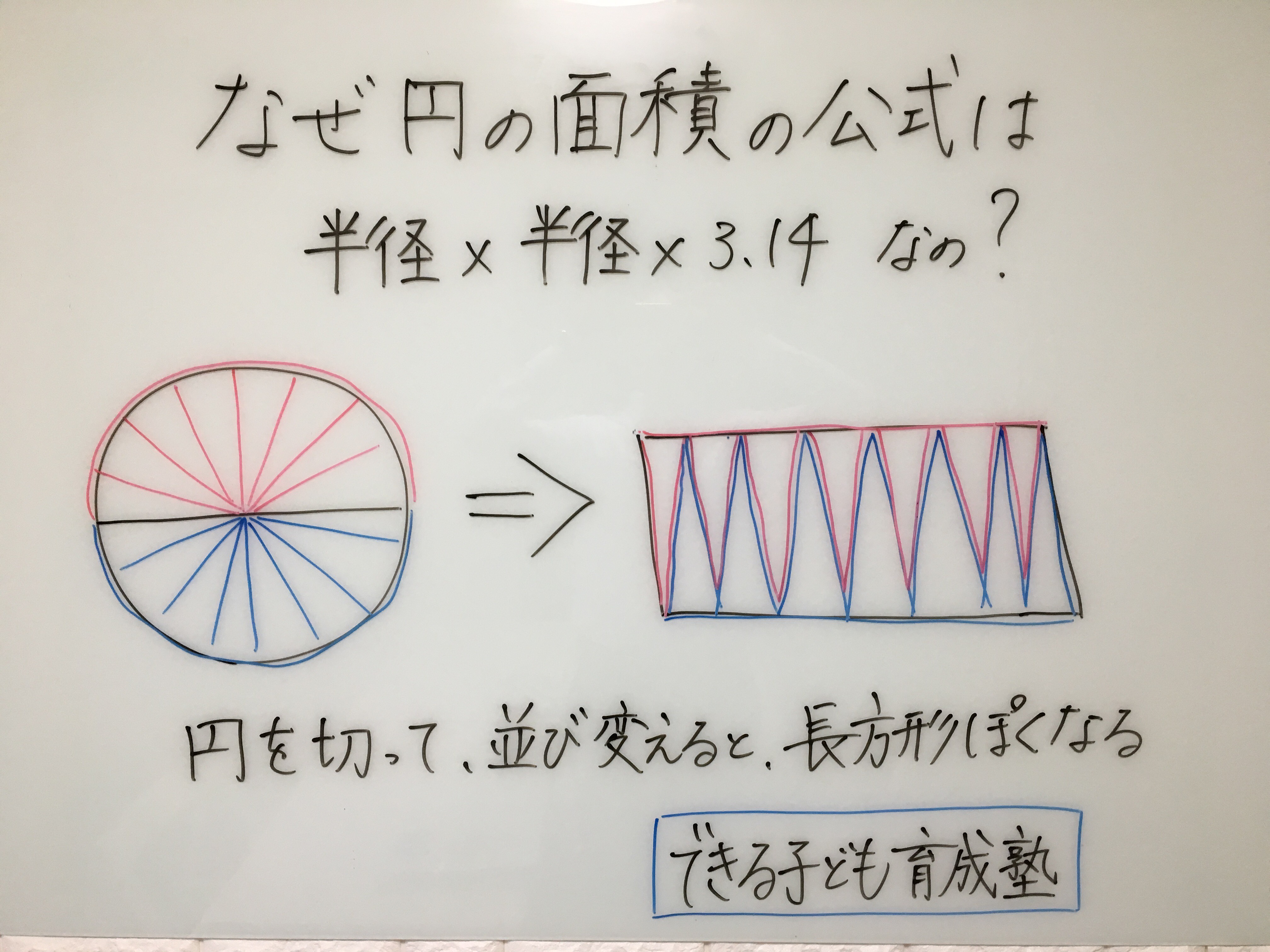



円の面積の求め方 公式 の理由を小学生に教える方法 元小学校教師が教える できる子ども育成塾 小岩 個別指導塾 小学生専門 国語と算数の苦手を克服
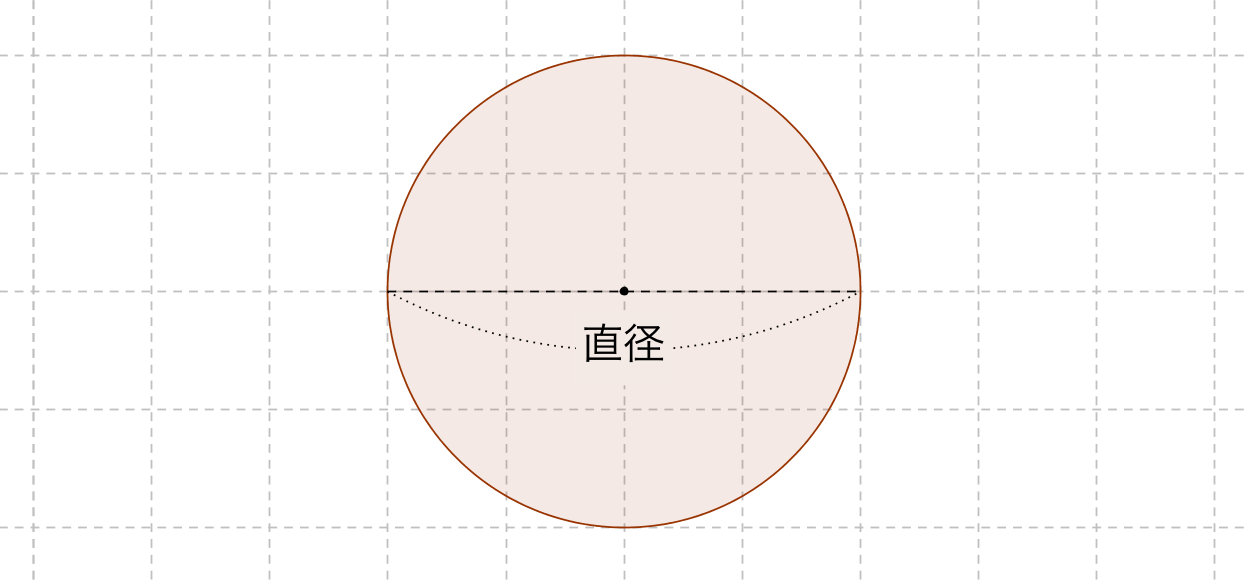



円周の公式 算数の公式
円形度 circularity (等面積円の円周)/(周長) 球の表面積 \(\pi D^2\) 球の体積 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3\) 球の質量 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3 \rho\) 球の体積基準比表面積(単位体積当たりの表面積) 1 numpypi 1つ目は、 numpypi を使う 方法です。 Numpyには、 numpypi という円周率の値を出してくれるやつが存在し、これを使うのが最も手っ取り早いです。 もはや計算すらしていないですねw Copied!円周角と中心角を使う円と半円の問題|中学数学の定期テスト対策 中学数学の定期テスト対策の範囲です。 円周角と中心角を使う円と半円の問題|高校入試レベルの難問まで 三平方の定理や面積比などもからめた、高校入試で見かける問題です。




円周率 算数用語集



この図形の円周の求め方を教えて下さい 円周というより 周 と Yahoo 知恵袋
ただし円周率は 314 とします。 円周を求める公式は 円周 直径 円周率 円 周 = 直 径 × 円 周 率 なので、 円周 円 周 = 56 × 314 = ( c m) になります。




円の面積の求め方 公式と計算例




円周と円の面積こんがらがらないように Explore Facebook



閲覧ありがとうございます 情報の問題です 円の円周と面積を繰り返し求めるフ Yahoo 知恵袋
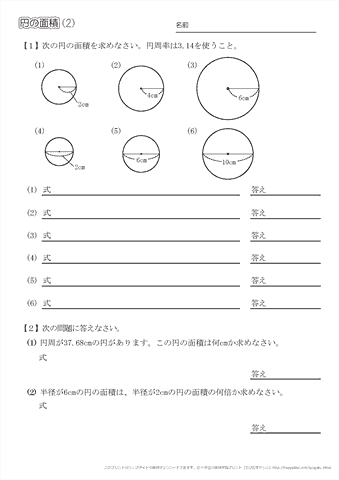



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




意外に知らない 知っていると得する 円の面積問題 恋する中高一貫校 適性検査 徹底攻略




円周 円の面積の求め方 チーム エン




円周の求め方と円の面積について アタリマエ



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun



六年生の算数の問題です 円の面積です 写真の を教えてください 式などもよ Yahoo 知恵袋




円 扇形 の面積 周や弧の長さの公式 数学fun



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




円の面積 円周の求め方 公式 小学生 中学生の勉強




円の面積を微分したら円周になる理由 Youtube




โน ตของ 円の面積のもとめ方 ช น Primary算数 Clearnote




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ



円の面積 半径
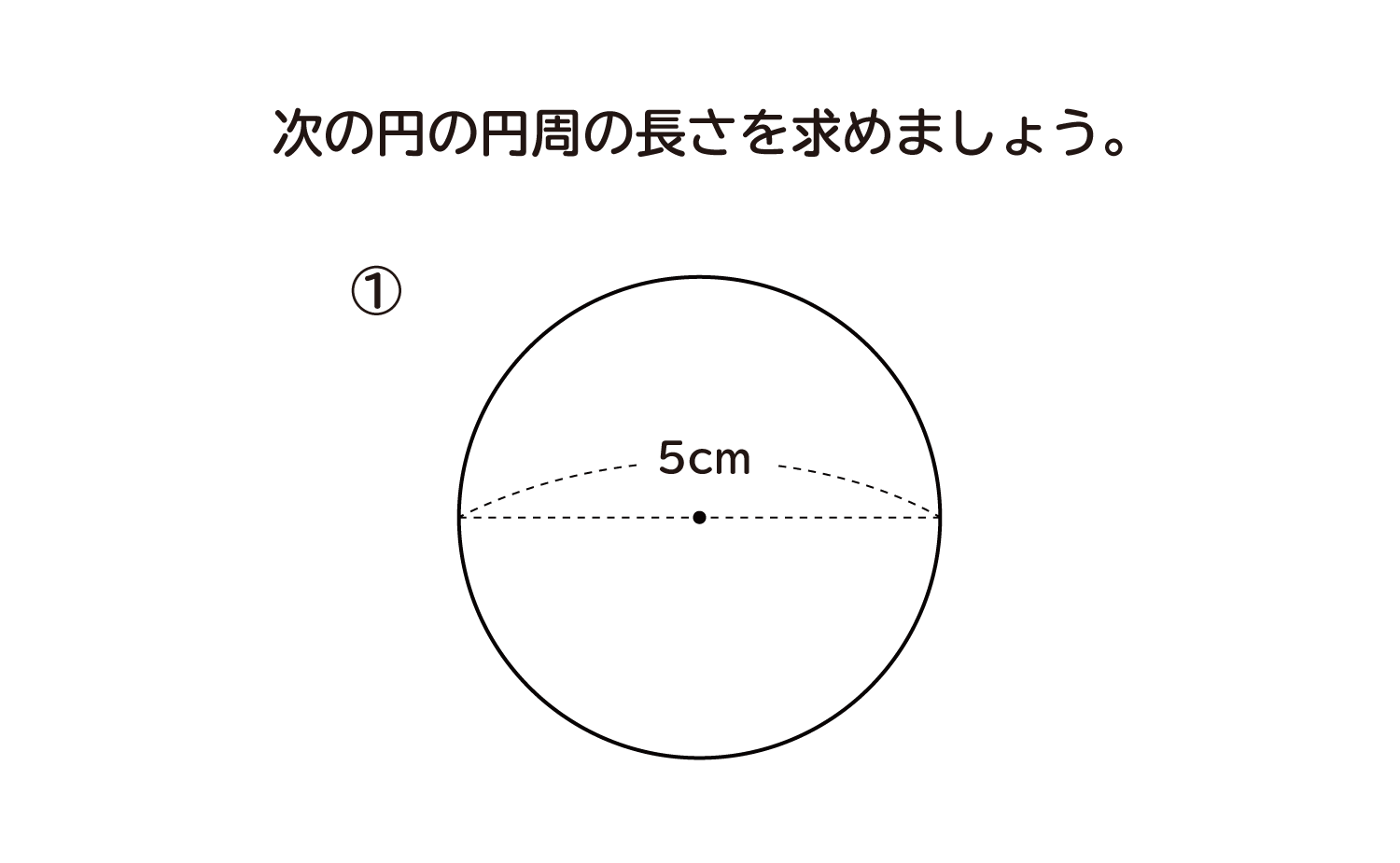



小学5年生 算数 無料問題集 円の直径と円周の長さ おかわりドリル




円の面積の求め方を自主学習ノートで復習しましょう 円の面積の基本的な練習問題 円の面積の求め方を確認しておきます 円の面積 半径 半径 円周率 ちなみに 円周の長さの求め方は 数学ノート 学習ノート 学習
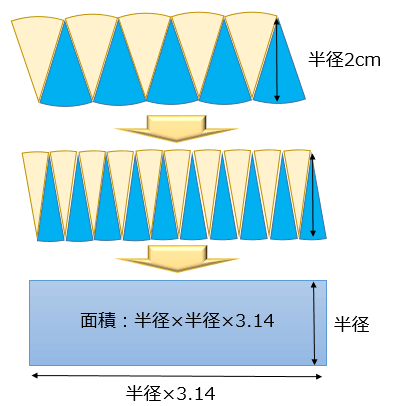



円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
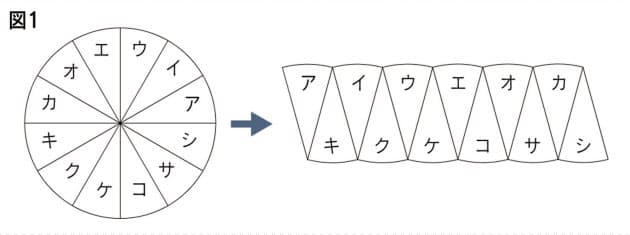



子供に説明できる 円の面積の公式 の証明 Nikkei Style
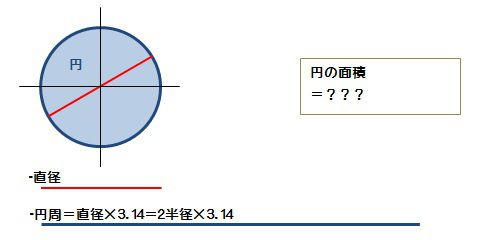



円の面積 算数の公式覚えてますか




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




円の面積 円周の求め方 公式 小学生 中学生の勉強
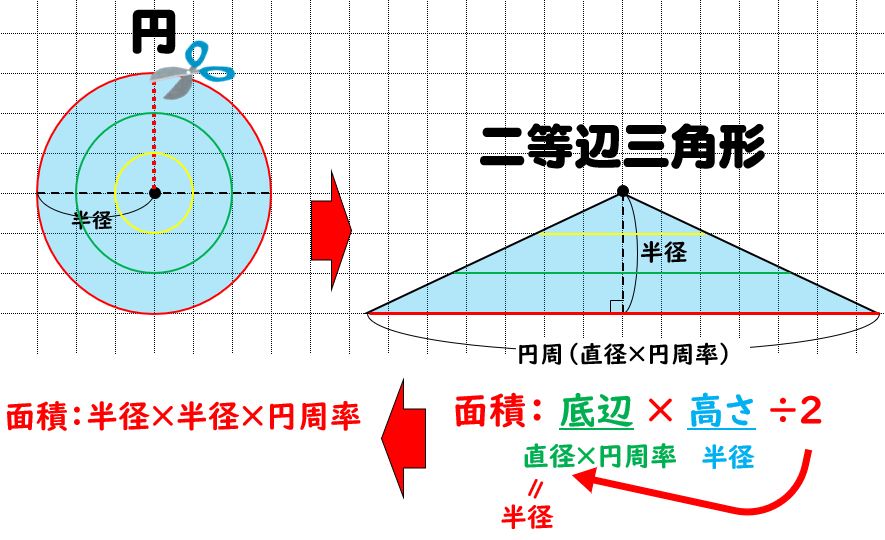



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円周と円の面積 計算ドリル 問題集 数学fun
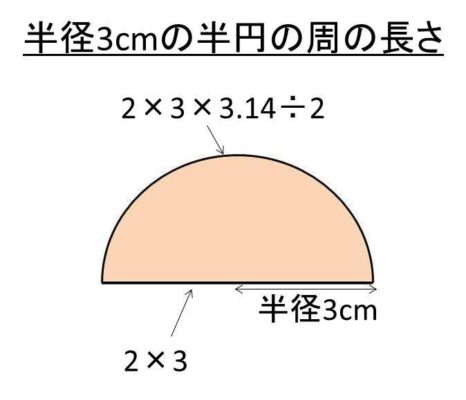



半円の周の長さの計算方法 白丸くん
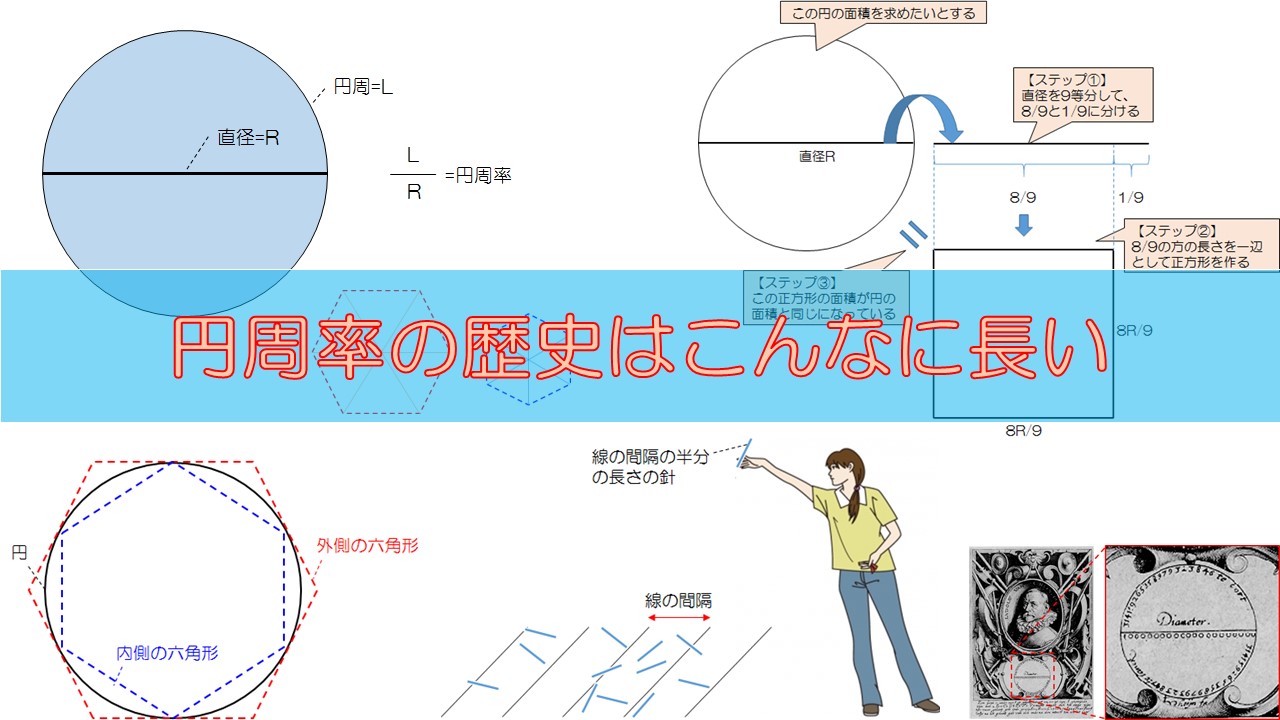



面白い円周率の歴史 昔の人たちはこうやって3 14 を求めてた 数学の面白いこと 役に立つことをまとめたサイト
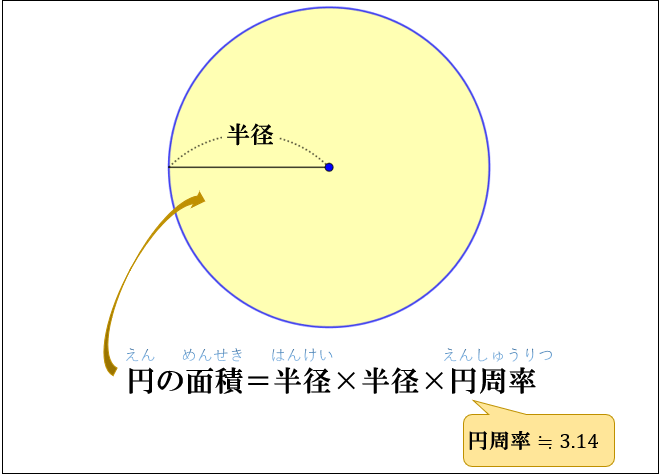



円周の求め方と円の面積について アタリマエ
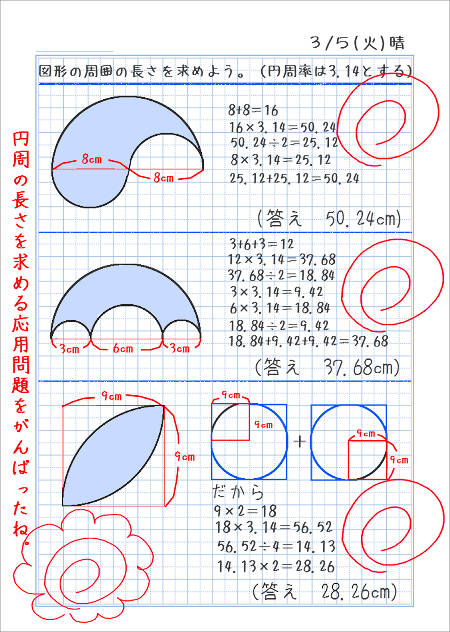



円周の長さの問題をもっと解いてみよう 家庭学習レシピ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ



気まぐれ Net 図を用いた円の面積の求め方 公式を使わずに
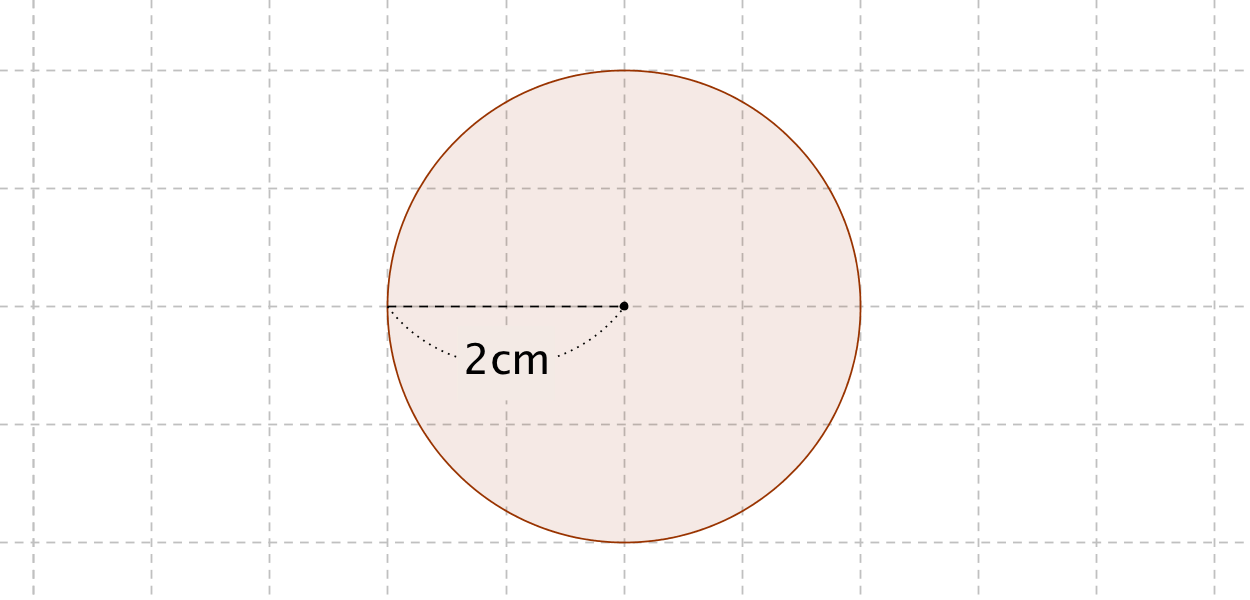



円の面積の公式 算数の公式




円の面積の求め方 公式と計算例



直径cmの円の周の長さと面積の求め方を式もありでお願いします Yahoo 知恵袋



6年算数 円の面積 2 わかる教え方
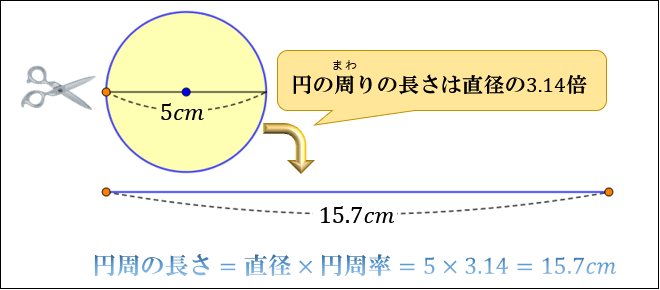



円周の求め方と円の面積について アタリマエ




小6 算数 小6 旧 円の面積 Youtube




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
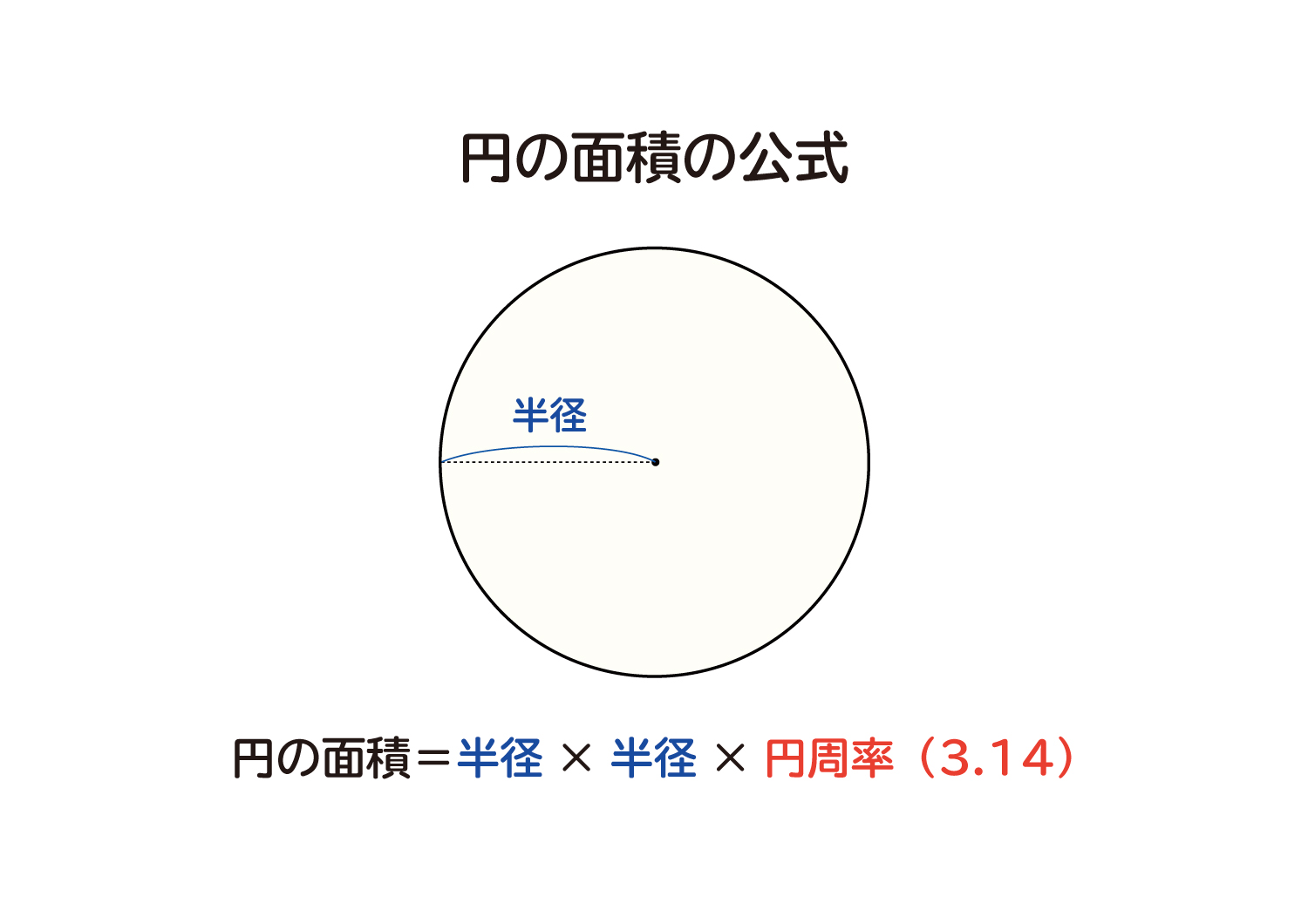



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




円の面積 算数用語集




円 扇形 の面積 周や弧の長さの公式 数学fun



面白い円周率の歴史 昔の人たちはこうやって3 14 を求めてた 数学の面白いこと 役に立つことをまとめたサイト




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




円の面積3 小学校6年生の教科書から つづき 身勝手な主張
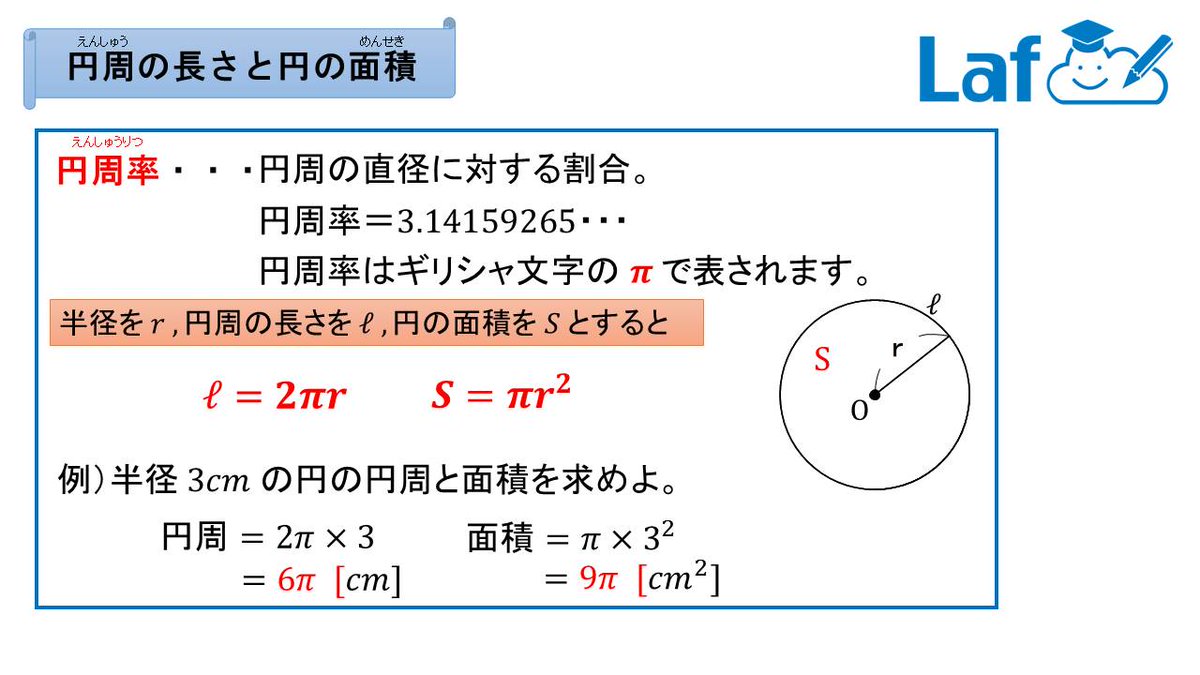



中学高校数学laf先生 質問回答中 中1数学 円周率p 円の面積 円周の長さ 1年生は事前に知っておいて損はなし 2年生は今のうちに軽く目を通して思い出しましょう 3年生は知っていたらrt 3年生は覚えてなかったらふぁぼって暗記




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円周 Wikipedia




円の面積 算数用語集




円の面積の応用 小学校6年算数より 身勝手な主張




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




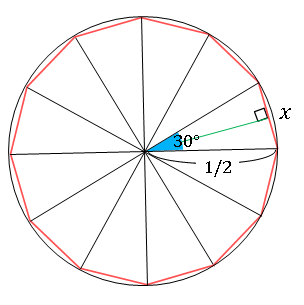
扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




円の面積の求め方 公式と計算例
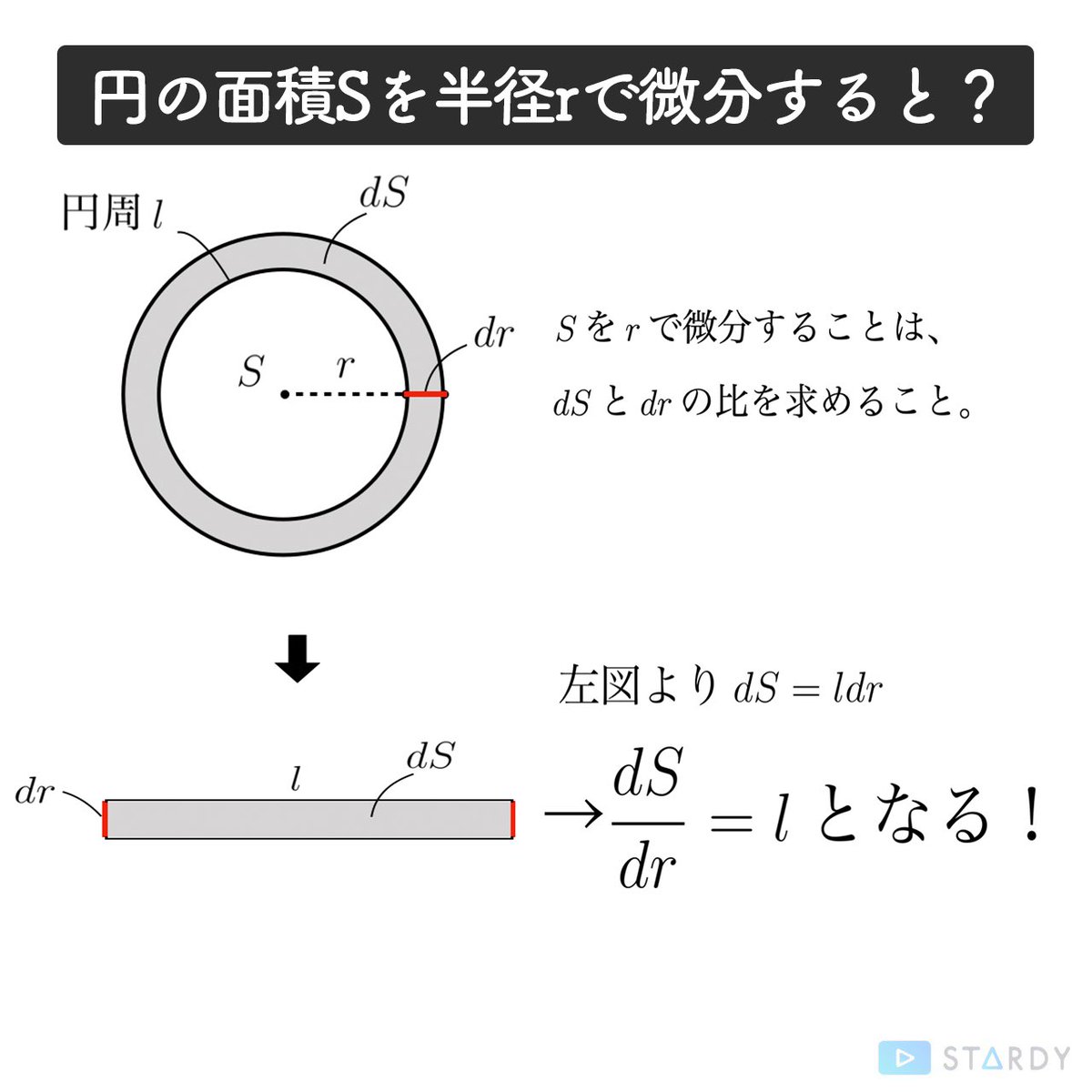



Stardy 実は円の面積を微分すると円周になると知っていましたか T Co Gisrglwseo Twitter




分かりません 教え下さい 明日までにお願いします Clearnote



円の面積の求め方




円周から直径を求める Youtube




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
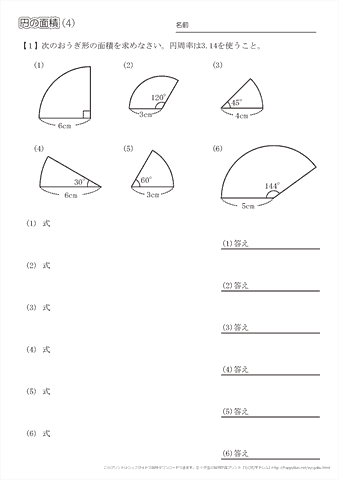



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



円の面積と周長 Excel Vba 数学教室




円の面積 練習応用 Youtube



円の面積 円周の求め方 公式 小学生 中学生の勉強




円周率 考 Jo談



円周の求め方と円の面積について アタリマエ




円の面積の求め方 公式と計算例



3



直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
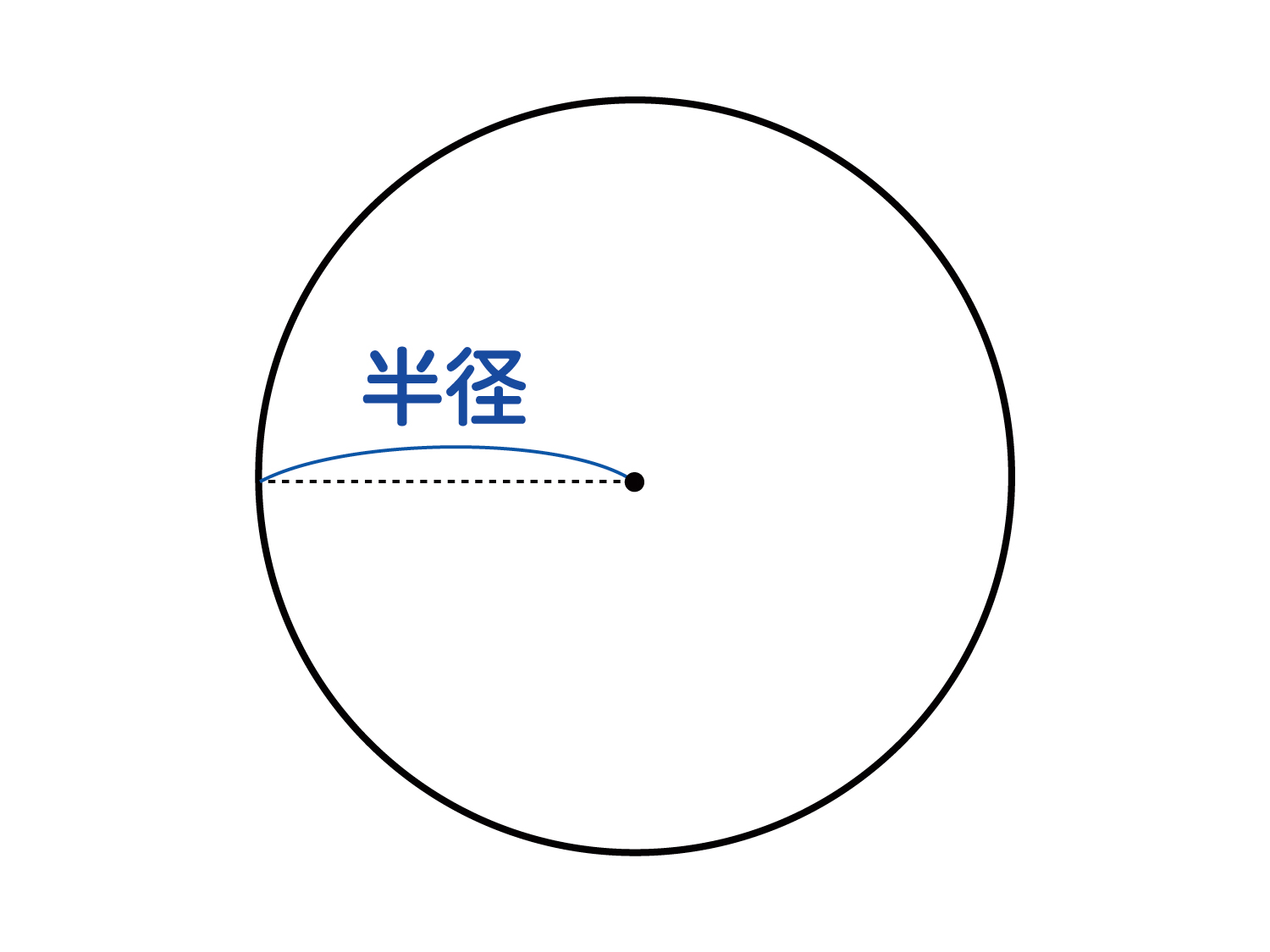



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




教えてください どうしても分からないんです 教えてください Clearnote




円周の求め方と円の面積について アタリマエ
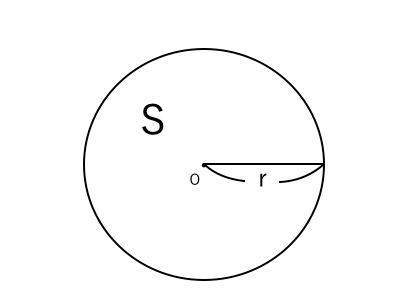



円の面積 円周の求め方 苦手な数学を簡単に




円周の求め方と円の面積について アタリマエ
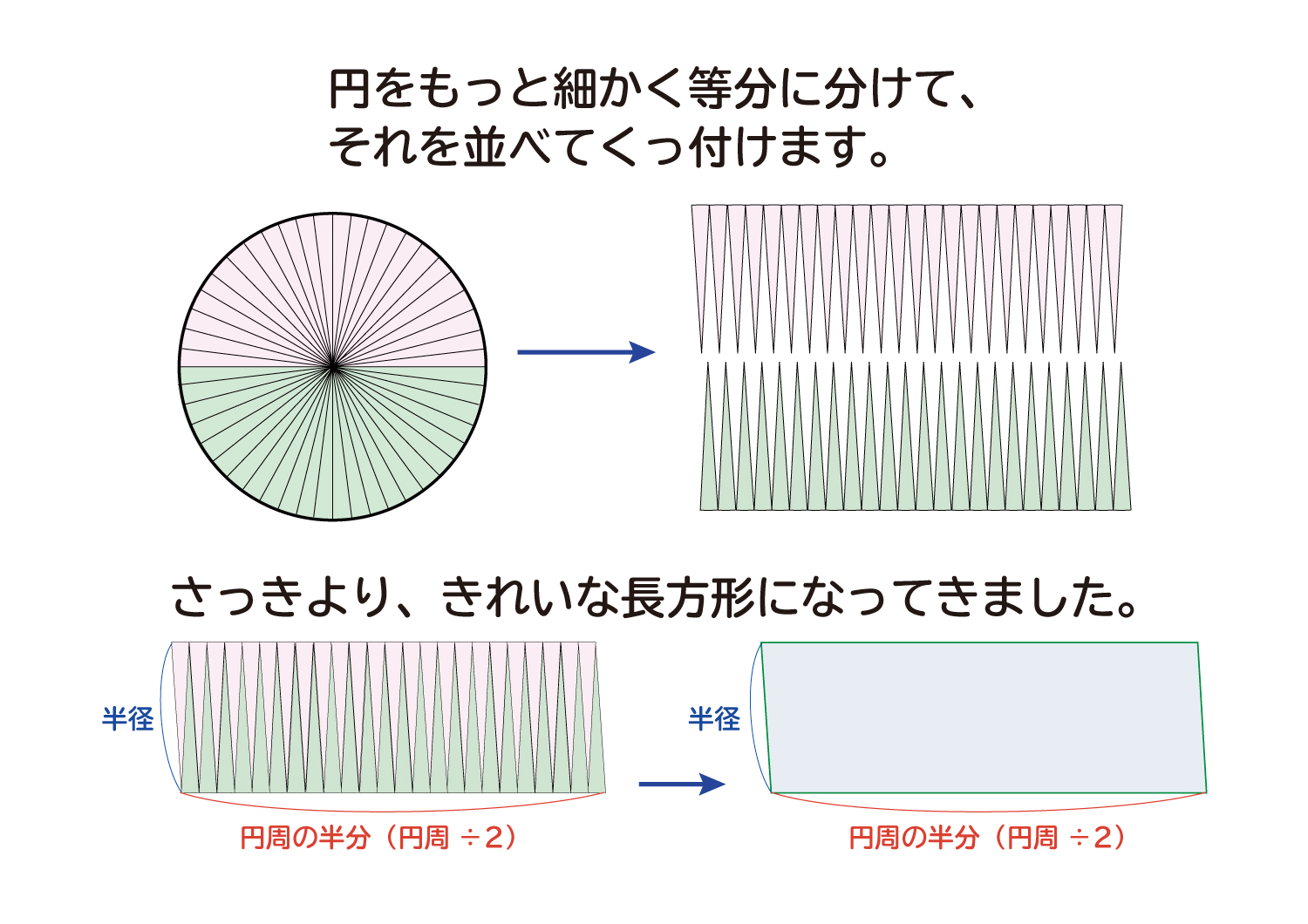



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




アスクル アーテック 円周と円の面積説明器 7649 直送品 通販 Askul 公式




円の面積応用b 学習ノート 学習 小学校 算数



円の面積の求め方 小学生
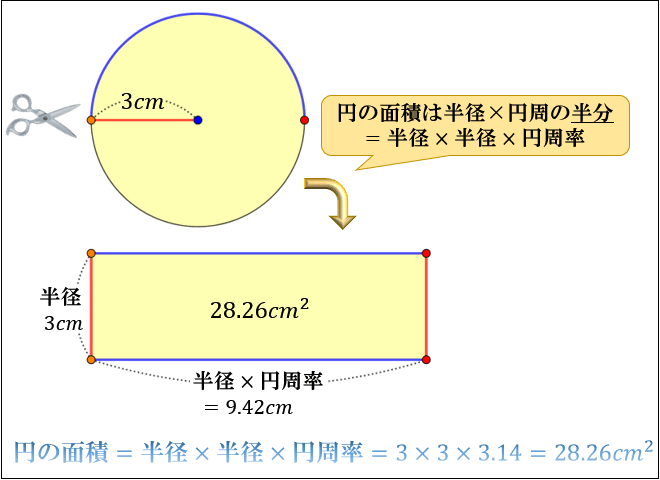



円周の求め方と円の面積について アタリマエ




スマホok 6年 円の面積 円の面積を求める公式 Youtube




円の面積 円周の求め方 公式 小学生 中学生の勉強



3




円の周りの長さを計算しよう 家庭学習レシピ




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




Amazon Co Jp アーテック 円周と円の面積説明器 おもちゃ




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4



0 件のコメント:
コメントを投稿